


|
<- Intervista agli organizzatori dell'OpenExp 2006 - Copertina - Una seconda occhiata a The Cathedral and the Bazaar -> |

|
PLUTOWare
L'articolo...In questo articolo facciamo una panoramica su alcune questioni importanti inerenti la programmazione in ambiente libero di un motore scacchistico. Data la vastità dell'argomento ci concentreremo solo su alcuni aspetti, considerando questo articolo come un'introduzione per il lettore interessato, in modo che possa approfondire le tematiche per conto proprio. Vedremo la struttura generale di un chess engine e gli aspetti essenziali dei componenti principali: la rappresentazione della scacchiera, il generatore delle mosse, l'algoritmo di ricerca e la funzione di valutazione della posizione. |
Lo scopo di questo articolo è illustrare il funzionamento interno di un chess engine. Prima però è opportuno fare qualche considerazioni di carattere generale. Un po' di pazienza e sarete ripagati.
Ci sono fondamentalmente tre diverse strategie per giocare a scacchi [9], le due prime proposte da Shannon nel suo classico articolo del 1950 [11]:
Ci concentreremo su la Strategia A, seguita da molti dei programmi liberi disponibili in rete, che è quella che probabilmente ha dato i migliori risultati.
Un chess engine ha quattro parti fondamentali [10]:
Il problema della rappresentazione della scacchiera è relativamente semplice, nel senso che implementare un sistema utilizzabile con un generatore di mosse generico non è complicato. È invece un problema difficile quello di sviluppare una rappresentazione efficiente della scacchiera.
Nella trattazione che segue considereremo la disposizione standard delle coordinate usata nella notazione algebrica:
Nero
a8 b8 c8 d8 e8 f8 g8 h8
a7 b7 c7 d7 e7 f7 g7 h7
a6 b6 c6 d6 e6 f6 g6 h6
a5 b5 c5 d5 e5 f5 g5 h5
a4 b4 c4 d4 e4 f4 g4 h4
a3 b3 c3 d3 e3 f3 g3 h3
a2 b2 c2 d2 e2 f2 g2 h2
a1 b1 c1 d1 e1 f1 g1 h1
Bianco
|
L'approccio che viene in mente per primo è quello di usare un array bidimensionale:
typedef enum {
VUOTA,
bR, bD, bT, bA, bC, bP,
nR, nD, nT, nA, nC, nP
} SQUARE;
SQUARE board[8][8];
|
con b e n che stanno per bianco e nero e la lettera maiuscola che indica l'iniziale del pezzo. board[0][0] corrisponde quindi alla casa a1 mentre board[7][7] alla casa h8.
Il problema è che questa rappresentazione è inefficiente, dato che per accedere alle caselle è necessario un doppio loop. Inoltre, dato che i moderni calcolatori immagazzinano gli array in forma di una lista lineare, essendo rig e col la riga e colonna di una determinata casella, per accedere ad essa il compilatore ha bisogno di una moltiplicazione e una addizione [6]:
rig * 8 + col |
oppure
rig << 3 + col |
che è meglio ma che richiede comunque un paio di istruzioni. Inoltre, per i pezzi che muovono in diagonale, abbiamo bisogno di testare continuamente che non siamo usciti fuori dalla scacchiera; ad esempio per le possibili mosse di un alfiere bianco situato nella casa e4 le case disponibili possono essere calcolate in questo modo:
int rig, col;
rig = 3;
col = 4;
for (;;) {
rig++;
col++;
if (rig > 7 || col > 7) {
break;
}
switch (board[rig][col]) {
case VUOTA:
/* casella vuota */
...
break;
case bR:
case bD:
case bT:
case bA:
case bC:
case bP:
/* pezzo proprio:
casella non disponibile */
...
break;
default:
/* pezzo dell'avversario */
...
break;
}
}
|
mentre per il movimento in diagonale in senso contrario abbiamo:
for (;;) {
rig--;
col--;
if (rig < 0 || col < 0) {
break;
}
switch (board[rig][col]) {
/* come prima */
...
}
}
|
Un discorso analogo vale per l'altra diagonale possibile. Gli if necessari per testare il bordo della scacchiera richiedono troppo tempo e fanno diventare l'intera procedura globalmente inefficiente.
La prima cosa da tener in considerazione per poter risparmiare tempo di calcolo è eliminare la doppia operazione (moltiplicazione/shift + addizione) che il compilatore deve fare quando lavora con array bidimensionali, ad esempio usando un array unidimensionale, più vicino a come la macchina immagazzina i numeri realmente:
SQUARE board[64]; |
con l'indice  i = 0  per la casella a1 e  i = 63  per la casella h8. Con un array unidimensionale, i possibili movimenti di un alfiere vengono generati aggiungendo o sottraendo 7 oppure 9 alla posizione di partenza, a seconda che si tratti, rispettivamente, di una diagonale parallela alla diagonale a8-h1 oppure alla diagonale a1-h8.
Rimane però il problema dei bordi della scacchiera. Si pensi ad esempio a un alfiere situato in f1 (i = 5) che si muove in diagonale verso g2 (i = 14) e h3 (i = 23). La casa successiva sarebbe per i = 23 + 9 = 32, che corrisponde alla a5, che è sbagliato. Bisogna quindi intercettare i bordi in maniera da produrre mosse legali.
Il modo classico di risolvere il problema è stato quello di aggiungere una "cornice" di caselle proibite [6,9], come illustrato di seguito:
99 99 99 99 99 99 99 99 99 99
99 99 99 99 99 99 99 99 99 99
8 99 . . . . . . . . 99
7 99 . . . . . . . . 99
6 99 . . . . . . . . 99
5 99 . . . . . . . . 99
4 99 . . . . . . . . 99
3 99 . . . . . . . . 99
2 99 . . . . . . . . 99
1 99 . . . . . . . . 99
99 99 99 99 99 99 99 99 99 99
99 99 99 99 99 99 99 99 99 99
a b c d e f g h
|
Il valore 99 ci consente di testare se la casella di destinazione è legale, all'interno di un array di 120 elementi anziché 64:
SQUARE board[120]; |
La cornice è larga due righe per ogni lato dato, che il cavallo può saltare anche due caselle in una direzione. Per le colonne è necessario solo una casella proibita per ogni lato, dato che gli indici sono consecutivi tra la fine della riga i sulla destra e l'inizio della riga i + 1 sulla sinistra, un'osservazione che permette di lavorare con un array di 120 elementi anziché 144 pur mantenendo una larghezza proibita di 2 caselle consecutive anche per le colonne.
Da tutte queste considerazioni abbiamo, per l'esempio del nostro alfiere in e4 (i = 28), quanto segue:
int casella;
casella = 28;
for (;;) {
casella += 9;
if (board[casella] == 99) {
break;
}
switch (board[casella]) {
/* uguale all'esempio degli
array bidimensionali */
...
}
}
for (;;) {
casella -= 9;
if (board[casella] == 99) {
break;
}
switch (board[casella]) {
/* uguale all'esempio degli
array bidimensionali */
...
}
}
|
Questa forma di rappresentazione è basata su una osservazione molto ingegnosa. Consideriamo la casa e4 (riga 3 e colonna 4, con gli indici che cominciano dallo 0, come è usuale nel C). Costruiamo un numero binario da 8 bit in cui i 4 bit più significativi rappresentano la riga e i 4 bit meno significativi la colonna:
$ bc obase=2 3 11 4 100 ibase=2 obase=A 00110100 52 |
Quindi, in questa rappresentazione, la casa e4 avrebbe l'indice 52 all'interno di un array unidimensionale di 128 elementi. Le restanti caselle della scacchiera avrebbero i seguenti indici:
8 112 113 114 115 116 117 118 119
7 96 97 98 99 100 101 102 103
6 80 81 82 83 84 85 86 87
5 64 65 66 67 68 69 70 71
4 48 49 50 51 52 53 54 55
3 32 33 34 35 36 37 38 39
2 16 17 18 19 20 21 22 23
1 0 1 2 3 4 5 6 7
a b c d e f g h
|
Come si può osservare, se consideriamo una determinata casella i allora le caselle in alto e in basso si ottengono facendo rispettivamente i + 16 e i - 16. Qual è il senso di tutto questo? Il fatto è che per ogni casella della figura precedente (una casella valida) si verifica:
i & 0x88 = 0 |
e per l'esempio dell'alfiere in e4 abbiamo qualcosa come:
int casella;
SQUARE board[128];
casella = 52;
for (;;) {
casella += 17;
if (casella & 0x88) {
break;
}
switch (board[casella]) {
...
}
}
for (;;) {
casella -= 17;
if (casella & 0x88) {
break;
}
switch (board[casella]) {
...
}
}
|
Si osservi che questo suppone un miglioramento in termini di velocità rispetto all'esempio dato per l'array unidimensionale. In entrambi i casi dobbiamo sommare o sottrarre una costante per ottenere l'indice della nuova casella di destinazione, ma per l'array unidimensionale abbiamo bisogno di testare il contenuto dell'elemento dell'array, scaricando il valore dalla memoria, mentre in questo caso abbiamo bisogno di lavorare solo con l'indice appena ottenuto.
Le bitboard sono forse il metodo oggi più utilizzato nella rappresentazione della scacchiera e la verifica delle mosse legali. Il principio è tanto semplice quanto geniale: una scacchiera contiene 64 caselle, quindi usiamo numeri di 64 bit per rappresentarle. Su un'architettura a 32 bit abbiamo:
typedef unsigned long long int BITBOARD; |
Il problema delle bitboard è che complicano di molto il codice, e sono molto meno intuitive e più difficili da seguire che l'utilizzo di semplici array, ma consentono di ottenere tutte le mosse valide, in una certa situazione, con una sola operazione logica a livello di bit. Ad esempio, la posizione di partenza:
8 1 1 1 1 1 1 1 1 7 1 1 1 1 1 1 1 1 6 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 a b c d e f g h |
verrebbe rappresentata dalla bitboard
11111111 11111111 00000000 00000000 00000000 00000000 11111111 11111111 |
All'interno del programma vengono costruite delle bitboard per fare fronte a necessità particolari: alcune avranno traccia della posizione di pezzi particolari (pedoni, cavalli, ecc.), altre conterranno informazioni di tutti pezzi, oppure di solo i pezzi bianchi o neri. Bisogna anche scegliere inizialmente alcune convenzioni, ad esempio quale casella rappresenta il bit più significativo. Nel nostro caso useremo il bit più significativo per la casella a1, e quello meno significativo per la casella h8. Questa convenzione è arbitraria e varia da programma a programma.
Cominciamo a vedere alcuni esempi di utilizzo delle bitboard. Consideriamo solo i pedoni del bianco nella posizione iniziale:
00000000 11111111 00000000 00000000 00000000 00000000 00000000 00000000 |
Questi pedoni possono avanzare uno o due passi, quindi passare alla situazione:
00000000 00000000 11111111 00000000 00000000 00000000 00000000 00000000 |
oppure
00000000 00000000 00000000 11111111 00000000 00000000 00000000 00000000 |
È chiaro che queste situazioni possono essere ottenute realizzando rispettivamente le seguenti operazioni a livello di bit:
BITBOARD pedoni_bianchi; pedoni_bianchi >> 8; pedoni_bianchi >> 16; |
A questo punto dovrebbe cominciare ad essere chiaro come funzionano le bitboard. Se ad esempio all'avvio del programma creiamo due bitboard contenenti i pezzi bianchi e neri nella posizione iniziale e le aggiorniamo man mano che si svolge la partita, possiamo ottenere le caselle vuote in qualsiasi momento della partita basandoci sulle due bitboard con:
BITBOARD caselle_vuote; caselle_vuote = ~(pezzi_bianchi | pezzi_neri); |
Per il movimento dei pedoni di due passi in avanti che abbiamo visto prima, le bitboard ci consentono di verificare facilmente quali pedoni non si sono mossi (altrimenti possono avanzare di un solo passo) con:
pedoni_bianchi & (255 << 48) |
dove 255 << 48 dà una riga di 1 tra a2 e h2. Ovviamente, un discorso analogo vale per il nero, tenendo conto che i bit da considerare saranno diversi. Le caselle disponibili (vuote) per il movimento in avanti dei pedoni bianchi di uno o due passi sono rispettivamente:
((pedoni_bianchi & (255 << 48)) >> 16) & (~tutti_pezzi) (pedoni_bianchi >> 8) & (~tutti_pezzi) |
Addentriamoci adesso un po' più in profondità nei meandri delle bitboard, dal punto di vista del codice. Cominciamo con alcune dichiarazioni:
typedef enum {
A1, B1, C1, D1, E1, F1, G1, H1,
A2, B2, C2, D2, E2, F2, G2, H2,
A3, B3, C3, D3, E3, F3, G3, H3,
A4, B4, C4, D4, E4, F4, G4, H4,
A5, B5, C5, D5, E5, F5, G5, H5,
A6, B6, C6, D6, E6, F6, G6, H6,
A7, B7, C7, D7, E7, F7, G7, H7,
A8, B8, C8, D8, E8, F8, G8, H8
} SQUARE;
typedef enum {COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8} COLUMN;
typedef enum {ROW1, ROW2, ROW3, ROW4, ROW5, ROW6, ROW7, ROW8} ROW;
|
Un primo grosso vantaggio nell'uso delle bitboard è quello che Hyatt chiama il "parallelismo sui bit" [5], che consiste nel fatto che in alcuni contesti possono essere generate tutte le mosse con una sola operazione a livello di bit. Un esempio è quello del movimento dei pedoni bianchi di uno o due passi che abbiamo appena visto: ciò fornisce contemporaneamente tutte le mosse degli 8 pedoni bianchi a partire dalla posizione iniziale. Un altro esempio di questo tipo è dato dalle considerazioni sui "pedoni passati": un pedone bianco passato in e4 ad esempio. "Passato" significa che non ci sono pedoni neri nelle caselle d5, d6, d7, e5, e6, e7, f5, f6, e f7. Per testare se il pedone in e4 è passato settiamo i bit per le caselle di interesse:
8 0 0 0 0 0 0 0 0 7 0 0 0 1 1 1 0 0 6 0 0 0 1 1 1 0 0 5 0 0 0 1 1 1 0 0 4 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 a b c d e f g h |
che produce una bitboard che chiameremo ped_pas[E4]:
00000000 00000000 00000000 00000000 00011100 00011100 00011100 00000000 |
Data una bitboard, pedoni_neri, contenente la configurazione dei pedoni neri nella posizione corrente, il test assume la seguente forma:
if (pedoni_neri & ped_pas[E4]) {
/* Il pedone E4 non è passato */
...
} else {
/* Il pedone E4 è passato */
...
}
|
Questo esempio dimostra il "parallelismo sui bit" di cui abbiamo parlato, dato che con una sola istruzione abbiamo in realtà risposto contemporaneamente a nove domande diverse. All'avvio del programma conviene inizializzare un array di 64 elementi con tutte le configurazioni possibili per i pedoni passati:
#define SHIFT64(x) (63 - x)
BITBOARD pedone_pass[64];
void init_bitboards_attacks(void) {
/* Inizializzazione bitboard per pedoni passati */
int i, j, sq;
BITBOARD unit = 1L;
const SQUARE pedone_pass_pos[9] = {
D5 - E4, E5 - E4, F5 - E4,
D6 - E4, E6 - E4, F6 - E4,
D7 - E4, E7 - E4, F7 - E4
};
const COLUMN col[64] = {
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8
};
const ROW row[64] = {
ROW1, ROW1, ROW1, ROW1, ROW1, ROW1, ROW1, ROW1,
ROW2, ROW2, ROW2, ROW2, ROW2, ROW2, ROW2, ROW2,
ROW3, ROW3, ROW3, ROW3, ROW3, ROW3, ROW3, ROW3,
ROW4, ROW4, ROW4, ROW4, ROW4, ROW4, ROW4, ROW4,
ROW5, ROW5, ROW5, ROW5, ROW5, ROW5, ROW5, ROW5,
ROW6, ROW6, ROW6, ROW6, ROW6, ROW6, ROW6, ROW6,
ROW7, ROW7, ROW7, ROW7, ROW7, ROW7, ROW7, ROW7,
ROW8, ROW8, ROW8, ROW8, ROW8, ROW8, ROW8, ROW8
};
for (i = 0; i < 64; i++) {
pedone_pass[i] = 0;
if (i < 8 || i > 47) continue;
for (j = 0; j < 9; j++) {
sq = i + pedone_pass_pos[j];
if (sq > 55 || abs(col[i] - col[sq]) > 1) continue;
pedone_pass[i] |= unit << SHIFT64(sq);
}
}
}
|
Questo pezzo di codice merita qualche spiegazione. Le dichiarazioni iniziali sono di per sé esplicative, l'unico punto importante è la costante:
const SQUARE pedone_pass_pos[9] = {
D5 - E4, E5 - E4, F5 - E4,
D6 - E4, E6 - E4, F6 - E4,
D7 - E4, E7 - E4, F7 - E4
};
|
la quale ci consente di definire la posizione dei pedoni avversari che non permettono il passaggio del pedone preso in considerazione. Questa dichiarazione ci permette di aggiungere ogni elemento dell'array a una casella data per ottenere tutte le case da tener d'occhio. Noi siamo partiti da un pedone situato in e4 come riferimento, ma la casella concreta che si usa non è rilevante dal momento che gli elementi vengono costruiti come differenze tra indici. Poi si entra in un ciclo che assegna il valore 0 ad ogni elemento dell'array di bitboard pedone_pass; a partire da questo valore "accenderemo" poi i bit giusti. Si noti che nella situazione corrente che stiamo analizzando, un pedone non può stare sulla prima o l'ultima riga e che un pedone bianco in penultima riga è per forza passato. Questo ci da l'occasione di evitare cicli inutili saltando tutte le case minori di 8 e maggiori di 47. Il secondo loop controlla a turno ognuno dei 9 elementi dell'array di costanti che abbiamo visto in precedenza, costruendo una nuova casa di destinazione a partire della posizione i corrente. Differenze tra i numeri di colonna della casella corrente e quella candidata sq maggiori di 1 vogliono dire che la casella i è situata al bordo della scacchiera e quindi la casella sq non costituisce un impedimento al passaggio del pedone considerato; inoltre un pedone bianco non può mai essere intralciato da un pedone nero situato in una casa di indice superiore a 55 perchè il pedone sarebbe su una traversa non permessa (l'ultima). Per ultimo, se la casella soddisfa tutte le condizioni, allora è possibile avere un pedone nero in quella posizione e accendiamo il bit nella posizione adeguata usando la macro SHIFT64, che tiene conto della nostra convenzione che il bit più significativo corrisponde alla casa a1.
Quanto visto è un esempio di inizializzazione delle bitboard per i pedoni passati. Ci conviene inizializzare anche le bitboard di tutte le possibili mosse dei pezzi in ognuna delle 64 caselle possibili. In modo analogo a quanto abbiamo visto per i pedoni passati:
BITBOARD cavallobb[64];
BITBOARD rebb[64];
BITBOARD pedonebb[64];
void init_bitboard(void) {
int i, j, sq;
BITBOARD unit = 1L;
const SQUARE pedonepos[2] = {C3 - B2, A3 - B2};
const SQUARE cavallopos[8] = {
B1 - C3, D1 - C3, A2 - C3, E2 - C3,
A4 - C3, E4 - C3, B5 - C3, D5 - C3
};
const SQUARE repos[8] = {
A1 - B2, B1 - B2, C1 - B2, A2 - B2,
C2 - B2, A3 - B2, B3 - B2, C3 - B2
};
const COLUMN col[64] = {
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8,
COL1, COL2, COL3, COL4, COL5, COL6, COL7, COL8
};
const ROW row[64] = {
ROW1, ROW1, ROW1, ROW1, ROW1, ROW1, ROW1, ROW1,
ROW2, ROW2, ROW2, ROW2, ROW2, ROW2, ROW2, ROW2,
ROW3, ROW3, ROW3, ROW3, ROW3, ROW3, ROW3, ROW3,
ROW4, ROW4, ROW4, ROW4, ROW4, ROW4, ROW4, ROW4,
ROW5, ROW5, ROW5, ROW5, ROW5, ROW5, ROW5, ROW5,
ROW6, ROW6, ROW6, ROW6, ROW6, ROW6, ROW6, ROW6,
ROW7, ROW7, ROW7, ROW7, ROW7, ROW7, ROW7, ROW7,
ROW8, ROW8, ROW8, ROW8, ROW8, ROW8, ROW8, ROW8
};
/* pedone init */
for (i = 0; i < 64; i++) {
pedonebb[i] = 0;
if (i < 8 || i > 55) continue;
for (j = 0; j < 2; j++) {
sq = i + pedonepos[j];
if (sq < 0 || sq > 63 || abs(col[i] - col[sq]) > 1) continue;
pedonebb[i] |= unit << SHIFT64(sq);
}
}
/* cavallo init */
for (i = 0; i < 64; i++) {
cavallobb[i] = 0;
for (j = 0; j < 8; j++) {
sq = i + cavallopos[j];
if (sq < 0 || sq > 63 || abs(col[i] - col[sq]) > 2 || abs(row[i] - row[sq]) > 2) continue;
cavallobb[i] |= unit << SHIFT64(sq);
}
}
/* re init */
for (i = 0; i < 64; i++) {
rebb[i] = 0;
for (j = 0; j < 8; j++) {
sq = i + repos[j];
if (sq < 0 || sq > 63 || abs(col[i] - col[sq]) > 1 || abs(row[i] - row[sq]) > 1) continue;
rebb[i] |= unit << SHIFT64(sq);
}
}
}
|
Per re e cavallo bisogna anche controllare che non ci siano salti oltre l'ultima traversa usando, in modo analogo a quanto abbiamo fatto per le colonne:
abs(row[i] - row[sq]) > 1 |
Il calcolo delle caselle attaccate da un pezzo avviene, come abbiamo già spiegato, sommando alla casella i ognuno degli elementi di un array di caselle ottenuto a partire da una casella arbitraria. Ad esempio, per il cavallo si tratta dell'array const SQUARE cavallopos[8] ottenuto a partire dalla casa c3:
8 . . . . . . . . 7 . . . . . . . . 6 . . . . . . . . 5 . X . X . . . . 4 X . . . X . . . 3 . . C . . . . . 2 X . . . X . . . 1 . X . X . . . . a b c d e f g h |
Per i pezzi diversi da pedone, re e cavallo, che possono "scivolare" di un numero arbitrario di caselle (in orizzontale, verticale e diagonale), cioè torre, alfiere e donna, il movimento è funzione di due parametri: la casella in cui si trovano e i pezzi presenti lungo la traiettoria. Il calcolo preliminare delle bitboard per inizializzare all'avvio del programma tutte le possibilità di movimento di questi pezzi deve tener conto di entrambi i parametri.
Una tecnica usata è quella del "grado di occupazione". Vediamo come viene applicata per il movimento orizzontale di una torre su una traversa. In pratica, consiste nel calcolare in anticipo un array di bitboard di 64 x 256 elementi. Ad esempio, per la torre, questo array rappresenta tutte le possibilità di occupazione della riga nella quale si trova la casella occupata dalla torre stessa:
BITBOARD torrebb[64][256]; |
Vediamo perché ci sono 256 elementi. Dobbiamo considerare le permutazioni di n elementi che si ripetono (cioè, ordinamenti che si differenziano gli uni dagli altri dall'ordine di successione dei loro elementi). Le permutazioni di n elementi a, b, c,... di cui a si ripete A volte, b si ripete B volte, ecc., è [2]:
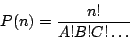
Per il problema del grado di occupazione, la natura dei pezzi non conta, ma solo se le case sono o non sono occupate. Quindi possiamo considerare le permutazioni di 2 elementi (casella vuota e casella occupata), che riempono una riga (8 caselle), e contiamo tutte le possibili permutazioni:
| Combinazione | Numero permutazioni |
|---|---|
| 8 caselle occupate | 8!/8! = 1 |
| 7 caselle occupate + 1 casella vuota | 8!/(7! x 1!) = 8 |
| 6 caselle occupate + 2 caselle vuote | 8!/(6! x 2!) = 28 |
| 5 caselle occupate + 3 caselle vuote | 8!/(5! x 3!) = 56 |
| 4 caselle occupate + 4 caselle vuote | 8!/(4! x 4!) = 70 |
| 3 caselle occupate + 5 caselle vuote | 8!/(3! x 5!) = 56 |
| 2 caselle occupate + 6 caselle vuote | 8!/(2! x 6!) = 28 |
| 1 casella occupata + 7 caselle vuote | 8!/(1! x 7!) = 8 |
| 0 caselle occupate | 8!/(6!) = 1 |
| TOTALE | 256 |
Di queste 256 permutazioni in realtà 128 potrebbero essere tolte, dato che una casella viene occupata dalla torre e non conta, e le caselle estreme potrebbero anche portare a una riduzione del numero di possibilità, ma visto che l'array di 64 x 256 viene costruito nella fase di inizializzazione del programma e non provoca ritardi durante la fase di calcolo, in realtà è comodo computare 256 bitboard per casella senza preoccuparsi di altre questioni.
Per calcolare il grado di occupazione possiamo utilizzare il seguente codice:
BITBOARD pezzi_bianchi, pezzi_neri, tutti_pezzi, occ; tutti_pezzi = pezzi_bianchi | pezzi_neri; occ = (tutti_pezzi >> (riga * 8)) & 255; |
dove riga è la traversa alla quale appartiene la casella i occupata dalla torre, per cui abbiamo la situazione di questo pezzo sulla riga considerata cercando nell'array l'elemento in precedenza calcolato di indice elemento[i][occ]. Con questa bitboard possiamo filtrare le catture ed i pezzi appartenenti al nostro bando con un semplice AND binario.
In questo caso, il codice di inizializzazione che abbiamo considerato nel paragrafo precedente potrebbe riportare quanto segue nella funzione init_bitboard per quanto riguarda il movimento orizzontale della torre:
/* torre, movimento orizzontale */
for (i = 0; i < 64; i++) {
for (j = 0; j < 256; j++) {
torrebb[i][j] = j << SHIFT64(8 * row[i]);
}
}
|
La tecnica del grado di occupazione è efficace per la rappresentazione dei movimenti orizzontali della torre. Ci sono da considerare anche i movimenti verticali, che in realtà seguono lo stesso principio. L'unica differenza riguarda la seguente disposizione delle caselle:
h8 h7 h6 h5 h4 h3 h2 h1 g8 g7 g6 g5 g4 g3 g2 g1 f8 f7 f6 f5 f4 f3 f2 f1 e8 e7 e6 e5 e4 e3 e2 e1 d8 d7 d6 d5 d4 d3 d2 d1 c8 c7 c6 c5 c4 c3 c2 c1 b8 b7 b6 b5 b4 b3 b2 b1 a8 a7 a6 a5 a4 a3 a2 a1 |
Si osservi che questa disposizione è ottenuta a partire dalla disposizione di partenza se ruotiamo la scacchiera di 90 gradi in senso orario. Si noti che le traverse di questa nuova scacchiera ruotata corrispondono alle colonne della scacchiera originale. Questa disposizione consente di utilizzare la tecnica del grado di occupazione per il movimento verticale della torre come se si trattasse di un movimento orizzontale, dal momento che la rotazione dispone in modo adiacente i bit che compongono le colonne della scacchiera di partenza.
A partire da questa nuova disposizione possiamo definire il seguente array:
const SQUARE board90[64] = {
H1, H2, H3, H4, H5, H6, H7, H8,
G1, G2, G3, G4, G5, G6, G7, G8,
F1, F2, F3, F4, F5, F6, F7, F8,
E1, E2, E3, E4, E5, E6, E7, E8,
D1, D2, D3, D4, D5, D6, D7, D8,
C1, C2, C3, C4, C5, C6, C7, C8,
B1, B2, B3, B4, B5, B6, B7, B8,
A1, A2, A3, A4, A5, A6, A7, A8
};
|
che utilizzeremo come traccia di quanto dobbiamo traslare per passare dalla scacchiera originale a quella ruotata, come vedremo più avanti. La prima casella della scacchiera normale (a1), che occupa il bit 0, ha invece il bit 7 (posizione h1 originale) nella scacchiera ruotata.
Utilizziamo lo stesso principio del movimento verticale della torre che abbiamo appena visto: ruotiamo la scacchiera in maniera da disporre i bit delle diagonali in modo adiacente e poter applicare la stessa indicizzazione degli array nella procedura di aggiornamento delle bitboard (grado di occupazione). In questo caso, realizziamo una rotazione di 45 gradi in senso antiorario e orario rispettivamente (per le due possibili diagonali che passano su ogni casella), e otteniamo:
h8 a8
g8 h7 a7 b8
f8 g7 h6 a6 b7 c8
e8 f7 g6 h5 a5 b6 c7 d8
d8 e7 f6 g5 h4 a4 b5 c6 d7 e8
c8 d7 e6 f5 g4 h3 a3 b4 c5 d6 e7 f8
b8 c7 d6 e5 f4 g3 h2 a2 b3 c4 d5 e6 f7 g8
a8 b7 c6 d5 e4 f3 g2 h1 a1 b2 c3 d4 e5 f6 g7 h8
a7 b6 c5 d4 e3 f2 g1 b1 c2 d3 e4 f5 g6 h7
a6 b5 c4 d3 e2 f1 c1 d2 e3 f4 g5 h6
a5 b4 c3 d2 e1 d1 e2 f3 g4 h5
a4 b3 c2 d1 e1 f2 g3 h4
a3 b2 c1 f1 g2 h3
a2 b1 g1 h2
a1 h1
|
A partire da queste nuove configurazioni possiamo scrivere le seguenti dichiarazioni:
const SQUARE board45a[64] = { /* rotazione 45 antiorario */
A1, C1, F1, B2, G2, E3, D4, D5,
B1, E1, A2, F2, D3, C4, C5, C6,
D1, H1, E2, C3, B4, B5, B6, A7,
G1, D2, B3, A4, A5, E6, H6, F7,
C2, A3, H3, H4, H5, G6, E7, B8,
H2, G3, G4, G5, F6, D7, A8, E8,
F3, F4, F5, E6, C7, H7, D8, H8,
E4, E5, D6, B7, G7, C8, F8, G8
};
const SQUARE board45o[64] = { /* rotazione 45 orario */
E4, F3, H2, C2, G1, D1, B1, A1,
E5, F4, G3, A3, D2, H1, E1, C1,
D6, F5, G4, H3, B3, E2, A2, F1,
B7, E6, G5, H4, A4, C3, F2, B2,
G7, C7, F6, H5, A5, B4, D3, G2,
C8, H7, D7, G6, A6, B5, C4, E3,
F8, D8, A8, E7, H6, B6, C5, D4,
H8, G8, E8, B8, F7, A7, C6, D5
};
|
che ci dà la posizione delle caselle della scacchiera originale in quelle ruotate; così ad esempio, la casella a1 della scacchiera originale è situata nella casella e4 in quella ruotata 45 gradi in senso orario. Unico particolare da tenere in considerazione: le diagonali non hanno tutte la stessa lunghezza. Conviene definire un array che specifica il numero di caselle di ogni diagonale, in maniera da evitare di usare caselle che appartengono alle diagonali superiore o inferiore a quella considerata.
È opportuno inizializzare array di bitboard che tengono conto della posizione di ogni casella nella scacchiera originale e in quelle ruotate, che poi ci serviranno per le nostre operazioni binarie di test sulle bitboard che contengono la disposizione dei pezzi. Le bitboard di questi array contengono un solo bit a 1, precisamente nella posizione specificata dalle dichiarazioni che abbiamo effettuato nelle sezioni precedenti:
BITBOARD bbmask[64], bbmask90[64], bbmask45a[64], bbmask45o[64];
for (i = 0; i < 64; i++) {
bbmask[i] |= unit << SHIFT64(i);
bbmask90[i] |= unit << SHIFT64(board90[i]);
bbmask45a[i] |= unit << SHIFT64(board45a[i]);
bbmask45o[i] |= unit << SHIFT64(board45o[i]);
}
|
Queste maschere ci servono per aggiornare delle bitboard di caselle occupate, secondo il seguente schema:
SQUARE da, a; caselle_occupate ^= bbmask[da] | bbmask[a]; |
che può essere usata se la casella di destinazione non è occupata (quindi la mossa non è una cattura). L'OR esclusivo mette a 0 il bit iniziale corrispondente alla casella da (che aveva inizialmente un 1 essendo occupata dal pezzo che stiamo muovendo) e mette a 1 il bit corrispondente alla casella a. La generazione delle bitboard ruotate ad ogni mossa è un'operazione inefficiente che richiede troppo tempo (bisogna aggiornare tutte le 64 caselle), per cui è meglio generare le bitboard ruotate delle caselle occupate all'avvio del programma e aggiornarle man mano che si generano le mosse. Analogamente a quanto abbiamo appena visto, possiamo fare:
caselle_occupate_90 ^= bbmask90[da] | bbmask90[a]; caselle_occupate_45a ^= bbmask45a[da] | bbmask45a[a]; caselle_occupate_45o ^= bbmask45o[da] | bbmask45o[a]; |
Quante bitboard ci conviene usare per il nostro programma? Hyatt ci suggerisce di usare 14 bitboard per i pezzi [6]: 6 per il Bianco e 6 per il Nero, contenenti le posizioni di pedoni, cavalli, alfieri, torri, donna e re, più due bitboard contenenti tutti i pezzi bianchi e tutti i pezzi neri. Inoltre, come abbiamo visto, è opportuno mantenere in memoria altre 4 bitboard contenenti le caselle occupate nella scacchiera normale e nelle 3 scacchiere ruotate [5].
Quanto abbiamo visto fino ad ora penso dia al lettore un'idea abbastanza precisa circa le possibilità espressive e la ricchezza delle bitboard. Le difficoltà supplementari alle quali ci conducono le bitboard vengono ripagate con un livello di astrazione e una concisione superiori. Tuttavia sarebbe un errore pensare che le bitboard siano una tecnica preferibile in tutti i casi. Per fare una scelta corretta della metodologia più adeguata, il programmatore deve fare un'analisi dell'hardware sul quale girerà il programma.
Tutto sommato le bitboard ci avvantaggiano solo se lavoriamo su hardware a 64 bit. Su macchine a 32 bit il processore dovrà in generale fare due operazioni di fetch per trasferire una unica bitboard dalla memoria ai suoi registri interni, aumentando il numero di cicli di clock necessari per realizzare tutte le operazioni. Quindi, su macchine a 32 bit il metodo del 0x88 può essere una tecnica utilizzabile da chi non voglia complicarsi la vita, essendo possibile ottenere prestazioni paragonabili all'utilizzo delle bitboard.
Naturalmente questo modo di lavorare non fa alcuna previsione sulla evoluzione del hardware. E' probabile che in un prossimo futuro assisteremo ad una proliferazione sempre più crescente delle macchine a 64 bit, il che ci consentirà di trarre il massimo vantaggio se avremo scelto la tecnica delle bitboard per il nostro programma.
Nella sezione precedente abbiamo visto come si fa a rappresentare e ad aggiornare le mosse. Il generatore delle mosse calcola in linea di principio tutte le mosse legali, queste vengono poi passate all'algoritmo di valutazione che si occupa di trovare la migliore continuazione. Il generatore usa le routine già viste per rappresentare e aggiornare le posizioni dei pezzi in memoria.
Si noti che nelle routine viste per aggiornare le bitboard non ci sono loop di alcun genere. Questa è una delle particolarità che rendono le bitboard interessanti. Per generare le mosse abbiamo invece bisogno di trovare i bit settati a '1' nelle bitboard dei pezzi che consideriamo. Ad esempio, il seguente codice dovuto a Nicola Rizzuti [10], che ringrazio, riporta un esempio di codice per generare le catture dei cavalli bianchi:
BITBOARD partenza, obiettivi;
int da, a;
/* estraiamo dalla struttura posizione
la bitboard dei cavalli bianchi */
partenza = pos->cavalli_bianchi;
/* iniziamo un ciclo che terminerà quando
non ci saranno più cavalli bianchi */
while (partenza) {
/* estraiamo dalla bitboard la casella in cui
si trova il primo bit pari a 1 */
da = firstbit(partenza);
/* trovato il bit lo cancelliamo in maniera da
non considerare due volte lo stesso pezzo */
partenza ^= maschera_casella[da];
/* calcoliamo i possibili obiettivi del cavallo
dalla casella in cui si trova */
obiettivi = cavallobb[da];
/* consideriamo soltanto le catture */
obiettivi &= pos->pezzi_neri;
/* iniziamo un secondo ciclo per scandire le
bitboard obiettivi e trova */
while (obiettivi) {
a = firstbit(obiettivi);
obiettivi ^= maschera_casella[a];
/* si inserisce la mossa nella struttura
scelta per rappresentarla */
...
}
}
|
La funzione firstbit è delicata, ed è quella che realizza la scansione della bitboard per trovare il primo bit pari a 1 (e quindi la posizione dei cavalli). Può essere implementata in diversi modi. Alcuni programmi, come Crafty (ftp://ftp.cis.uab.edu/pub/hyatt/), usano le istruzioni bsf e bsr dell'assembly in una dichiarazione inline, che è efficiente ma dipendente dall'hardware e ci obbliga ad usare nel nostro programma il preprocessore e una compilazione condizionale.
Per generare le mosse di non cattura, basta sostituire la riga
obiettivi &= pos->pezzi_neri; |
con
obiettivi &= ~(pezzi_bianchi | pezzi_neri); |
A partire dalla generazione delle mosse possibili è necessario disporre di un algoritmo che ci possa indicare la "mossa migliore" tra tutte quelle possibili. L'algoritmo usato viene denominato Minimax [7,12], e fu applicato alle strategie di gioco inizialmente da Shannon e Turing. Nei giochi a "informazione perfetta", cioè che hanno le seguenti caratteristiche [3]:
il teorema del Minimax permette in linea di principio a ciascun giocatore di giocare in modo ottimale, sempre che il gioco rispetti i seguenti vincoli [1]:
Per ogni sua possibile strategia un giocatore considera tutte quelle che può mettere in atto l'avversario e la massima perdita che potrebbe derivargli; egli sceglierà poi la strategia per cui tale perdita è minima. Questa, che minimizza la massima perdita, è ottimale per entrambi i giocatori se essi hanno Minimax uguali (in valore assoluto) e contrari (in segno) [8].
Per esemplificare come funziona il Minimax, consideriamo la seguente Figura:

Il punteggio finale indica la valutazione calcolata per ogni posizione. In ogni configurazione, il Bianco tenta di massimizzare il proprio punteggio e il Nero di minimizzarlo. Quindi il Bianco sceglierà mosse che producano il punteggio più alto possibile ma considerando che il Nero giocherà al meglio e che quindi sceglierà la migliore continuazione per se stesso.
Facciamo un esempio semplice con i rami più a sinistra della Figura. Consideriamo le sequenze 1.d4 d5 2.c4 e 1.d4 d5 2.Cf3, sulle quali abbiamo considerato due possibili mosse per il Nero. Le possibilità che abbiamo sono:
| Sequenza | Punteggio |
|---|---|
| 1.d4 d5 2.c4 dxc4 | +0.1 |
| 1.d4 d5 2.c4 e6 | +0.2 |
| 1.d4 d5 2.Cf3 Cf6 | +0.25 |
| 1.d4 d5 2.Cf3 e6 | -0.55 |
Considerando solo queste possibilità, per il Bianco la continuazione migliore sarebbe 1.d4 d5 2.Cf3 Cf6, che dà un punteggio di +0.25. Ma abbiamo detto che dobbiamo considerare che il Nero gioca di forma perfetta, per cui dopo 1.d4 d5 2.Cf3, il Nero non giocherà 2. ... Cf6, ma 2. ... c6, che lo porta in vantaggio (-0.55). Quindi, il Bianco farà 1.d4 d5 2.c4, a cui il Nero risponderà con 2. ... dxc4 se gioca correttamente. Questo è il punto: minimizzare le perdite. Naturalmente, considerando l'intero albero di varianti si aumentano le complessità di calcolo e il numero di possibilità da valutare, ma la sostanza del metodo rimane invariata.
Il seguente pseudocodice, dovuto a Nicola Rizzuti [10], implementa l'algoritmo Minimax:
Maximize(posizione p) {
if (verifica_fine_gioco(p)) {
return(Valore(p));
}
max_valore = -infinito;
Genera_successori(p);
for (tutti i successori) {
search = Minimize(ognuno dei successori);
max_valore = Max(max_valore, search);
}
return(max_valore);
}
Minimize(posizione p) {
if (verifica_fine_gioco(p)) {
return(Valore(p));
}
min_valore = +infinito;
Genera_successori(p);
for (tutti i successori) {
search = Maximize(ognuno dei successori);
min_valore = Min(min_valore, search);
}
return(min_valore);
}
|
Il seguente pseudocodice di Nicola Rizzuti implementa invece un modo per compattare il codice precedente ed l'algoritmo Negamax:
Negamax(posizione p) {
if (stop_search(p)) {
return(Valutazione(p));
}
gamma = -infinito;
Genera_successori(p);
for (tutti i successori) {
search = -Negamax(ognuno dei successori);
gamma = Max(gamma, search);
}
return(gamma);
}
|
Minimax e Negamax sono algoritmi sicuri, nel senso che offrono una risposta deterministica "esatta" all'interno di un albero di varianti, secondo i criteri implementati nella funzione di valutazione. Il problema è che in questa forma sono inapplicabili nella pratica: un albero di varianti con un fattore di ramificazione m (numero medio di mosse possibili ad ogni turno) e profondità t contiene mt posizioni da esplorare [9]. Tenendo conto della profondità di gioco (intesa come numero di mosse in avanti) necessaria per raggiungere un livello di gioco medio-alto, il numero di configurazioni da valutare diventa ingestibile anche per i più potenti calcolatori. Si rende necessario un criterio che permetta la valutazione di un sottoinsieme delle possibilità con probabilità minima di trascurare mosse forti.
La potatura Alfa-Beta implementa una semplificazione nelle ricerche Minimax. Il nome dell'algoritmo fu dato da Shannon, che chiamò Alfa al valore della migliore continuazione del Bianco e Beta a quello del Nero. Ne parleremo solo brevemente.
Supponiamo che la profondità dell'analisi sia pari a 3 (due mosse) e che il numero medio di mosse possibili sia 38. Allora, il Bianco studierà una delle mosse possibili (prima variante) e le 38, in media, possibili risposte del Nero. In questo modo determinerà qual è la mossa del Nero che gli dà la migliore valutazione. Successivamente, il Bianco studia un'altra delle sue mosse possibili (seconda variante) e le 38, in media, possibili risposte. Supponiamo adesso che, tra queste, la terza risposta del Nero nella seconda variante dia a questo colore una valutazione migliore della sua migliore risposta al Bianco nella prima variante. In questo caso sarebbe una perdita di tempo continuare a cercare risposte al movimento del Bianco nella seconda variante, dato che rappresenta per il Bianco l'essere in svantaggio rispetto alla prima variante: è meglio passare alla terza variante. Con questa decisione abbiamo risparmiato 35 delle risposte possibili alla mossa del Bianco nella seconda variante.
Il Minimax fornisce lo stesso risultato con o senza potatura Alfa-Beta; l'unica differenza è che con l'Alfa-Beta lo raggiungerà prima. Inoltre, l'efficacia dell'algoritmo Alfa-Beta dipende dall'ordine nel quale vengono considerate le mosse. Se in ogni punto dell'albero si considera per prima la migliore mossa del colore che deve giocare, allora la ricerca si riduce da mt a 2mt/2. La seguente Tabella dà un' idea della riduzione fornita dalla potatura Alfa-Beta supponendo un fattore di ramificazione di 38:
| Mosse in avanti | mt | 2mt/2 | % rispetto al totale |
|---|---|---|---|
| 2 | 1444 | 76 | 5.26 |
| 3 | 54872 | 468 | 0.85 |
| 4 | 2085136 | 2888 | 0.14 |
| 5 | 79235168 | 17802 | 2.25E-2 |
| 6 | 3010936384 | 109744 | 3.64E-3 |
L'ultima colonna riporta la percentuale di posizioni da valutare rispetto al totale mt. Questi valori sono veri solo se, come abbiamo detto, si considera per prima la migliore mossa in ogni punto di valutazione, e questo sarà in generale falso, per cui il numero di posizioni da valutare sarà compreso tra 2mt/2 e mt. L'efficacia della procedura dipenderà da come il programma ordina le mosse possibili, il che avviene in genere secondo criteri euristici.
Dove risiede la "intelligenza" di un chess engine? Non di certo negli aspetti che abbiamo studiato finora: rappresentazione della scacchiera e funzione di ricerca, anche se un' implementazione efficiente di questi aspetti consente di valutare più mosse per unità di tempo (più mosse "in avanti") e implicitamente aumentare la forza di gioco. Ken Thompson dimostrò come la considerazione di ogni mossa completa in più (mossa del Bianco + mossa del Nero) nella profondità dell'albero di varianti fa guadagnare circa 200 punti Elo nella forza di gioco del programma [3].
La forza di un chess engine risiede nella capacità di assegnare i punteggi alle posizioni generate, in modo che un algoritmo di ricerca come Minimax o Negamax possa prendere le decisioni corrette. Cioè risiede nella funzione di valutazione. Si noti che Minimax è matematicamente sicuro "data una funzione di valutazione"; se questa fa considerazioni scorrette sui punteggi relativi delle diverse configurazioni raggiunte, allora Minimax ci fornirà mosse deboli e il nostro programma giocherà male.
Matematicamente, la funzione di valutazione ha la forma di una somma ponderata:
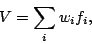
dove le fi sono funzioni base che considerano i diversi aspetti del gioco. L'importanza di ognuno di questi aspetti viene fornito dai valori dei pesi wi, i quali possono avere segni diversi per entrambi gli avversari. Il valore di V viene in genere valutato in base a posizioni statiche; se arrivati alla profondità massima prefissata ci si trova a un punto dell'albero di varianti che contiene una posizione non statica (ad esempio, si è in mezzo a una sequenza di catture), allora si aumenta la profondità dell'analisi in modo arrivare a una posizione statica che permetta l'applicazione della equazione precedente.
Ad esempio, Shannon [11] propose di usare una funzione di valutazione che conteneva le seguente funzioni base:

con le maiuscole e minuscole che rappresentano i parametri per entrambi gli avversari. Come si può osservare, il peso maggiore è dovuto allo squilibrio materiale; quando il materiale è equilibrato, la posizione viene valutata in base a considerazioni strettamente posizionali.
È più forte il cavallo del Bianco o l'alfiere del Nero in questa posizione? Questo pedone isolato è realmente debole? Queste sono le domande alle quali una funzione di valutazione deve poter dare una risposta adeguata. Contrariamente a quanto si possa pensare, la differenza tra un Maestro e un giocatore di club risiede principalmente nella differenza di sensibilità per giudicare questo tipo di aspetti posizionali più che nella capacità di calcolo.
La funzione di valutazione del nostro programma potrebbe tenere in considerazione più cose. Ad esempio Beowulf (http://www.frayn.net/beowulf/index.html), il programma libero dietro a ChessBrain, un progetto distribuito per gli scacchi il cui server è attualmente in fase di test [4], considera tra altre cose:
Tradizionalmente i valori relativi dei coefficienti dei termini nella funzione di valutazione venivano scelti attraverso un lavoro nel quale un Maestro tentava di far capire al programmatore come considerare tutti questi aspetti in maniera corretta. Naturalmente, non possiamo ingaggiare un Maestro per mettere in piedi il nostro programma casalingo. È possibile, tuttavia, scegliere i coefficienti attraverso una procedura automatica (un programma). Questa procedura richiede però del calcolo differenziale ed esula dallo scopo di questo articolo.
La lunghezza di parola del sistema che stiamo usando è importante, tra le altre cose, nella dichiarazione delle bitboard. In base al sistema, è possibile costruire un Makefile con definizioni personalizzate per il compilatore che consentano una compilazione condizionale. Passando a gcc parametri come -DBIT32 o -DBIT64, possiamo utilizzare le seguenti istruzioni per il preprocessore:
#ifdef BIT32
typedef unsigned long long int BITBOARD;
#elif BIT64
typedef unsigned long int BITBOARD;
#endif
|
dove abbiamo considerato che il tipo di dato int nella nostra macchina a 64 bit occupa 32 bit, come succede realmente in molti ambienti. Se anche int occupa 64 bit, useremo semplicemente
typedef unsigned int BITBOARD; |
I programmi che al loro interno usano mappe di bit, come i chess engine, sono particolarmente influenzati dall'ordine con cui l'hardware immagazzina i dati. Nella nostra discussione sulle bitboard abbiamo scelto il bit più significativo per la casella a1 in una macchina Little-endian a 32 bit. Per un computer Big-endian la situazione dei bit più e meno significativi è rovesciata, e ne dobbiamo tener conto nelle nostre operazioni di shift sui bit. In genere viene usata la compilazione condizionale, attraverso l'utilizzo di definizioni del tipo -DLITTLE_ENDIAN o -DBIG_ENDIAN.
Il seguente codice (http://en.wikipedia.org/wiki/Endianness),
rilasciato sotto la licenza GFDL (http://en.wikipedia.org/wiki/Wikipedia:Text_of_the_GNU_Free_Documentation_License)
realizza un check che verifica se l'hardware è Little-endian o
Big-endian.
#define LITTLE_ENDIAN 0
#define BIG_ENDIAN 1
int machineEndianness() {
int i = 1;
char *p = (char *) &i;
if (p[0] == 1) /* Lowest address contains the least significant byte */
return LITTLE_ENDIAN;
else
return BIG_ENDIAN;
}
|
È opportuno che il programmatore tenga in mente alcuni dettagli importanti riguardanti la portabilità del programma su hardware a 64 bit. Naturalmente queste indicazioni sono valide per qualunque programma, ma è facile che un chess engine deva poter girare anche su macchine a 64 bit. Ad esempio, se vogliamo iscrivere il nostro programma a uno dei tornei che si fanno su Internet, è molto probabile che gli organizzatori usino hardware a 64 bit e pretendano che il programma sia compilato per questo ambiente. Alcune indicazioni importanti possono essere:
Il mio scopo è stato quello di evidenziare le problematiche che un chess engine pone dal punto di vista dello sviluppo. Spero di esserci riuscito almeno in parte. I problemi da risolvere e le tecniche che nel tempo sono state sviluppate hanno interesse dal punto di vista strettamente informatico; all'interno di tecniche note l'implementazione efficiente di queste è comunque un tema interessante per un programmatore. Un chess engine offre un campo di prove ottimo per chi vuole familiarizzare ed imparare definitivamente a realizzare operazioni a livello di bit, oppure implementare alberi binari ed ennari in memoria per realizzare ricerche efficienti, oltre ad offrire un'occasione per considerare seriamente i problemi sulla portabilità, che in un chess engine diventano forse più contingenti che in altri programmi.
Abbiamo tralasciato tante cose interessanti: la costruzione degli indici di hashing per le tabelle di trasposizione (un argomento importantissimo all'interno degli algoritmi di ricerca in generale), l' implementazione dei libri di aperture e le basi di dati di finali, le diverse euristiche sviluppate per migliorare il Minimax e l'Alfa-Beta ecc., ma avrebbero allungato ancora di più questo articolo con questioni al di fuori dell'interesse del Pluto Journal. Tra le citazioni e la bibliografia troverete comunque delle ottime risorse per approfondire questi argomenti.
L'autoreFrancisco Yepes Barrera è socio di ILS ed appassionato per diletto e per lavoro di informatica e di scienze. I suoi interessi riguardano la computazione scientifica, l'intelligenza artificiale e l'utilizzo di software libero nella soluzione di problemi matematici. |

|
<- Intervista agli organizzatori dell'OpenExp 2006 - Copertina - Una seconda occhiata a The Cathedral and the Bazaar -> |

|